Mercury transit of 9 May 2016 Parallax using the solar granulation
As with transits of Venus, transits of Venus can in principle be used to determine the astronomical unit (au), which is a measure of the average distance of the Earth from the Sun. Historically, however, such measurements have not been made with transits of Mercury since that planet is much smaller and farther away, giving a much lower expected accuracy. Measuring the astronomical unit from the transit of Mercury was one of the planned experiments for the 9 May 2016 transit.
Up to 1700 UTC, the transit was photographed through an H-alpha filter. The hope that simultaneous images could be found from an extreme southern site, such as South Africa, were not fulfilled. Amateur astronomers in the Republic of South Africa responded with friendly answers and also a few pictures, but the resolution both spatially and temporally were not sufficient for the measurement.
Image created by Johan Moolman, of
Pretoria,
South Africa. Sent by Allan Versfeld
From 17:00 UTC onward, the transit was changed to a visual filter. An 800 mm f/15 FH-refractor was used with a Herschel-diagonal. This system provides an optimum contrast. The goal was to map Mercury as it passed over the granulation. From 15:00 UTC, Mercury was also seen in the United States, and we hoped that comparison with American images would allow the parallax to be measured.
Indeed,
we are able to use a
series of CCD observations (made also
into a video) that was taken at the Big Bear Solar Observatory (BBSO)
in California, an observatory run by the New Jersey Institute of
Technology. Credit for the images go to Jay Pasachoff of Williams
College and Caltech, Glenn Schneider of the Steward Observatory of
the University of Arizona, and BBSO personnel Dale Gary, Bin Chen,
Claude Plymate, Vasyl Vurchyshyn and
John Varsik. They have a 1.6-m
New Solar Telescope with adaptive optics (http://bbso.njit.edu).
The
video is available at:
http://nicmosis.as.arizona.edu:8000/ECLIPSE_WEB/TOM2016/BBSO_BW_TOM2016_BACK_END_ALIGNED.mov
For the measurement, we used a BBSO image from 16:29:35 UTC. Of course, the resolution from Germany was much worse, since it was only a small amateur telescope compared with the Big Bear Solar Observatory’s large professional telescope. Nevertheless, enough similarities in the granulation can be seen to allow the two images to be overlain.
The
distance between the middle of the discs is 132 pixel. The diameter of
Mercury is 180 pixel or 12.1 arcseconds. So the distance of both discs
is 8,87
arcseconds.
The
calculation is made with https://www.luftlinie.org/Europa/Usa
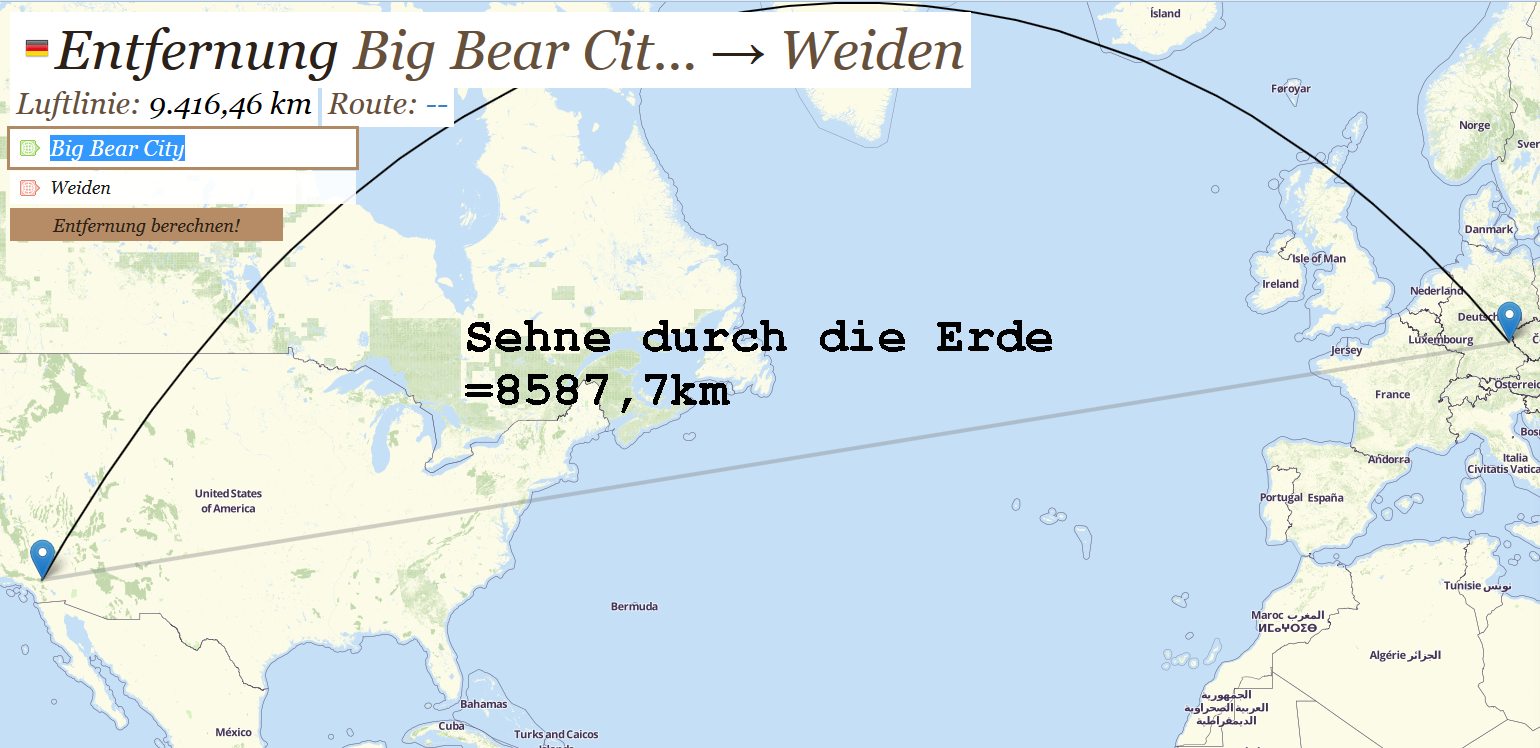
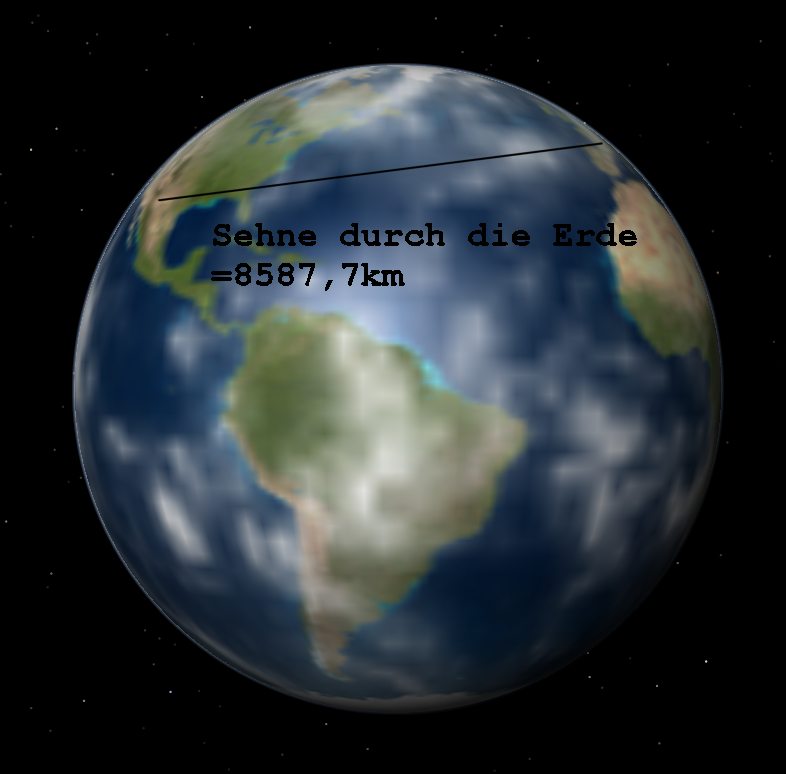
The distance between the sites in Weiden, Germany, and Big Bear Solar Observatory, California, was determined to be 9416 km. But relevant is the line through the earth. It´s calculated to 8587.7 km. The value would correspond to the direction of the Sun when it is at the same height above the horizon. However, the German measurements were with the Sun 19.35° above the horizon while the BBSO measurements were made with the Sun 43.7° above the horizon. The difference of 24.35° shortens the line of sight from the perspective of the sun to cos(24.35°)*8587.7 = 7824 km.
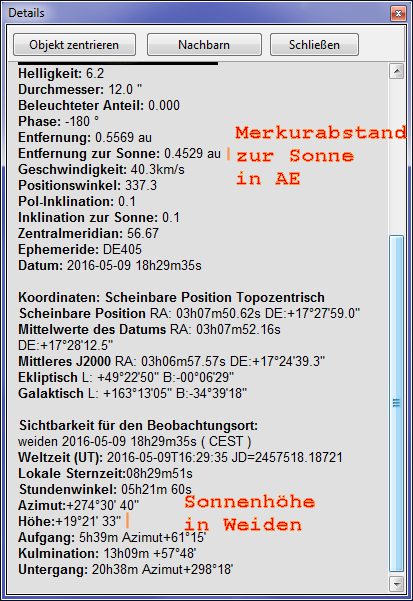
To determine the astronomical unit in linear units like kilometers, we
first calculate the distance from Mercury to the Sun in au, using the
orbital period and Kepler’s third law. The orbit of Mercury,
however, is highly elliptical. Therefore, the actual distance is
variable. For simplicity we used a value from Cartes du Ciel.
Accordingly, the distance from the Sun to Mercury on the day of the
transit was 0.4529 au. Anyone interested in the calculation according
to Kepler can look at the website: http://www.astrode.de/venustr2.htm.
The calculation of the au is based on Kepler’s third law.
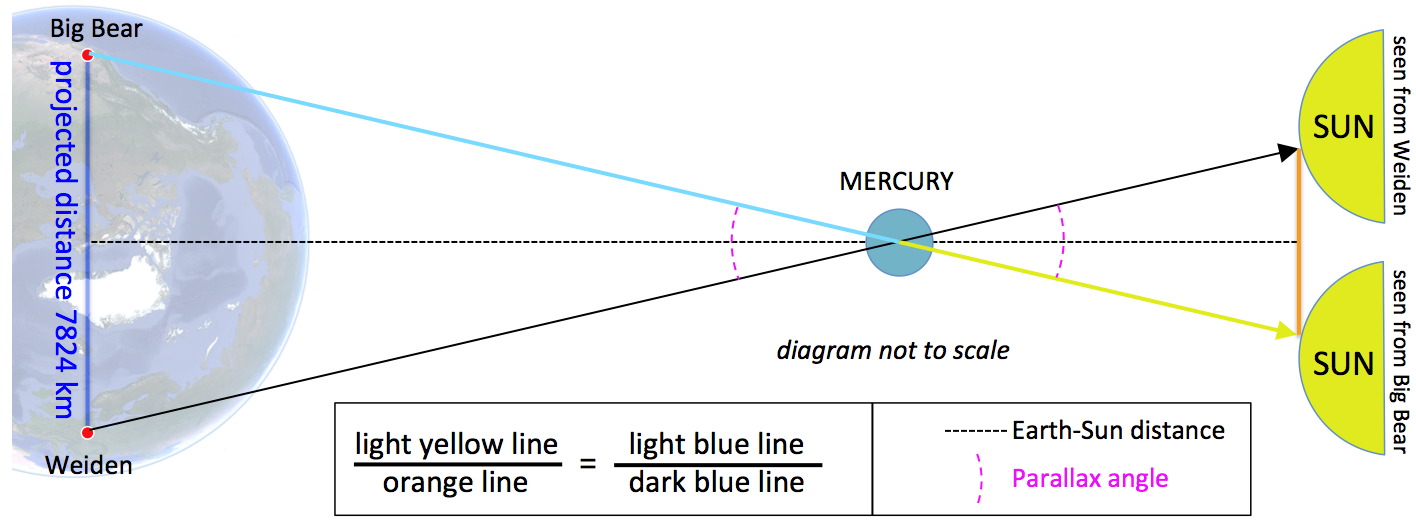
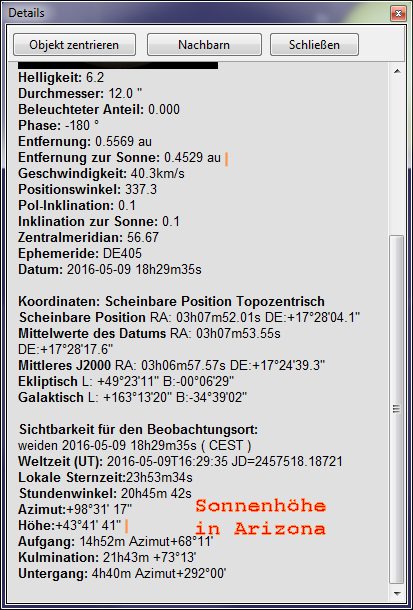
Now, the parallax of the Sun corresponds to the half-angle of the Earth from the point of view of an observer on the Sun. With a diameter of 12757 for the Earth and a distance of 0.4529 au from Mercury to the Sun, the solar parallax is 8.73 arcseconds. With the au, we can now calculate the diameter of the Earth directly from the solar parallax.
Astronomical unit = diameter of the Earth /tan(solar parallax / 3600 * 2).
The result is a value of 150.7 million km.
Because
of Mercury’s elliptical orbit, the distance on the day
of the transit was larger than the astronomical unit of 149.6 million
kilometers; it was 1.0097 au or 151,050,000 km. The variation in the
distance determination is only 0,23 percent!
This high accuracy is probably just a fluke. The distance between
the two disk centers can be best determined only to the nearest 5%. We
must assume, therefore, that the error bars are similarly high.
