Merkurtransit
9.5.2016
Parallaxenmessung mit Hilfe der Sonnengranulation


Ähnlich wie der Venustransit kann auch der Merkurtransit genutzt werden um die astronomische Einheit zu bestimmen, die den Abstand der Erde von der Sonne wiedergibt. Historisch ist der Merkurtransit jedoch ohne Bedeutung. Der Planet ist viel kleiner und weiter entfernt. Daher ist die zu erwartende Messgenauigkeit viel geringer. Das es dennoch im Prinzip möglich ist mit dem Merkur zu messen war eines der geplanten Experimente zum Transit vom 9.5.2016.
Bis 17 Uhr wurde mit einem H-Alpha-Filter fotografiert. Die Hoffnung das sich zeitgleiche Bilder in Südafrika finden lassen erfüllte sich leider nicht. Auf eine Anfrage bei Amateurastronomen in der RSA gab es zwar freundliche Antworten und auch ein paar Bilder, doch die Auflösung und die Zeiterfassung waren für die Messung nicht ausreichend.
Image created by Johan Moolman, of Pretoria, South Africa. Send by Allan Versfeld.
Ab 17 Uhr wurde von H-Alpha auf visuell umgestellt. Hierbei wurde ein 80mm f/15 FH-Refraktor mit einem Herschelkeil verwendet. Dieses System liefert einen optimalen Kontrast. Ziel war es Merkur vor der Granulation abzubilden. Ab 15 Uhr UT war Merkur auch in den USA zu sehen und es besteht die Hoffnung das sich jenseits des Atlantik Bilder finden lassen um die Parallaxe auszumessen.
Tatsächlich
fanden
sich einige Doppel zu einem Video das am BigBearSolar-Observatory in
Kalifornien
entstanden ist.
http://nicmosis.as.arizona.edu:8000/ECLIPSE_WEB/TOM2016/BBSO_BW_TOM2016_BACK_END_ALIGNED.mov
Für
die Messung
wurde ein Foto von 16:29:35 UT verwendet. Natürlich ist die
Aufnahme aus Deutschland viel schlechter in der Auflösung.
Hier
wurde lediglich eine kleine Amateuroptik verwendet
während in Kalifornien ein professionelles
Großteleskop
zur
Verfügung stand. Dennoch lassen sich ausreichend
Ähnlichkeiten erkennen, um eine Überlagerung zu
ermöglichen.



Der Abstand zwischen den Mittelpunkten der Scheibchen liegt auf dem folgenden Bild bei 132 Pixeln. Der Merkur selbst bietet sich als Referenz an. Er ist 180 Pixel groß. Die 180 Pixel entsprechen 12,1 Bogensekunden. Die beiden Scheibchen sind also 8,87 Bogensekunden voneinander entfernt.

Nun muss noch der Abstand zwischen den Standorten in Weiden/Deutschland und BigBearCity in Kalifornien bestimmt werden. Die Luftline beträgt 9416,46 km. Die Berechnung erfolgte mit https://www.luftlinie.org/Europa/Usa
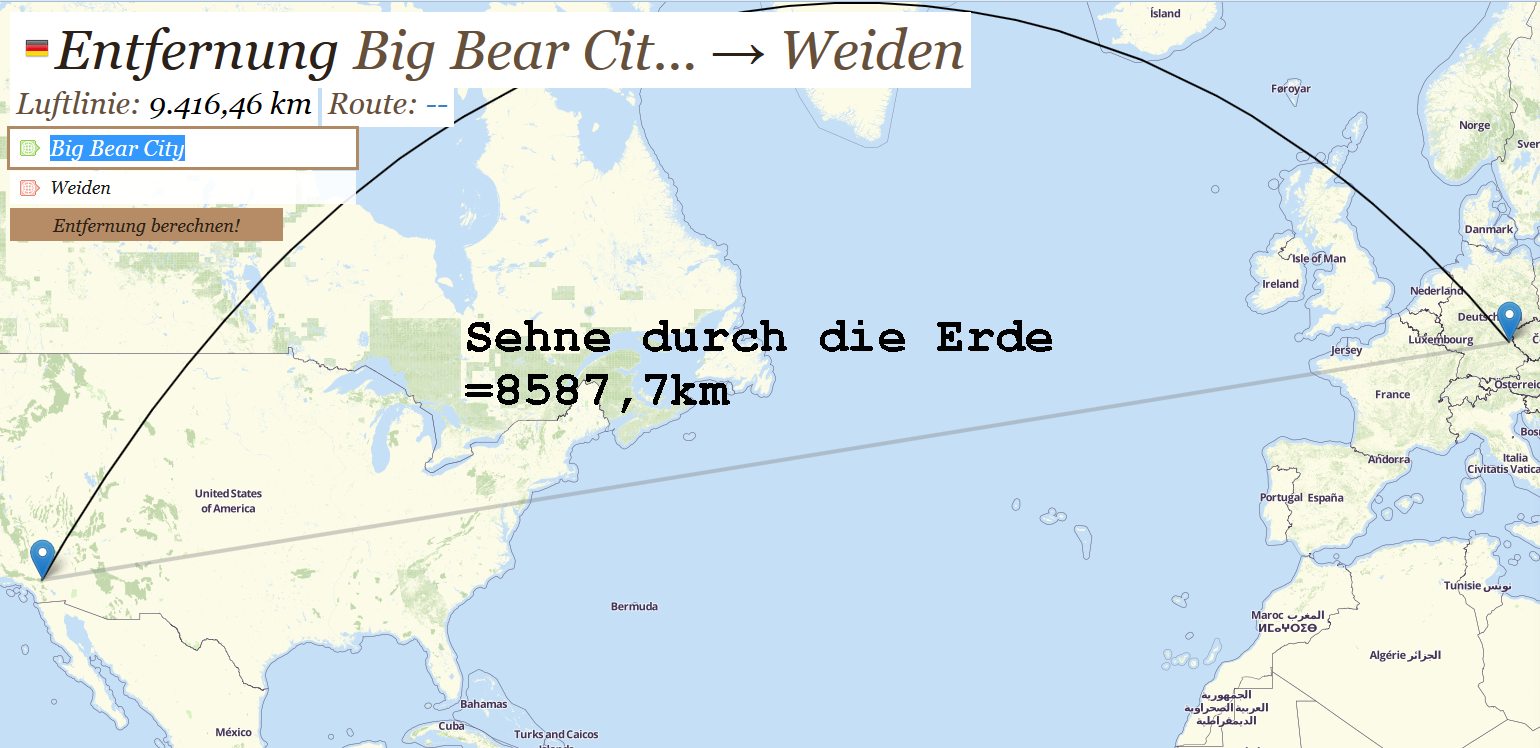
Relevant ist jedoch die Sehne durch die Erde. Sie kann mit dem Sinussatz auf 8587,7 km berechnet werden.
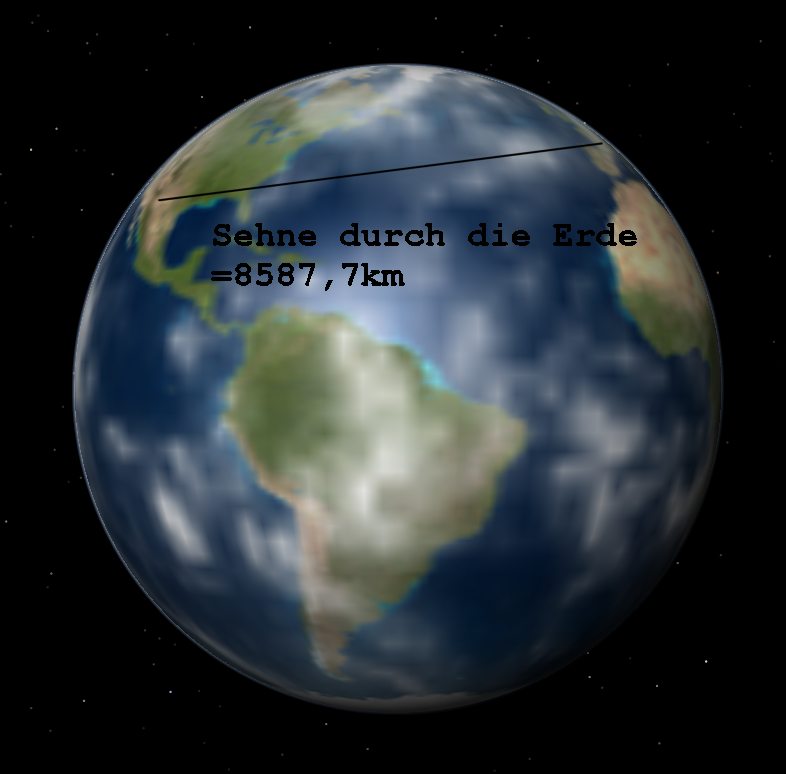

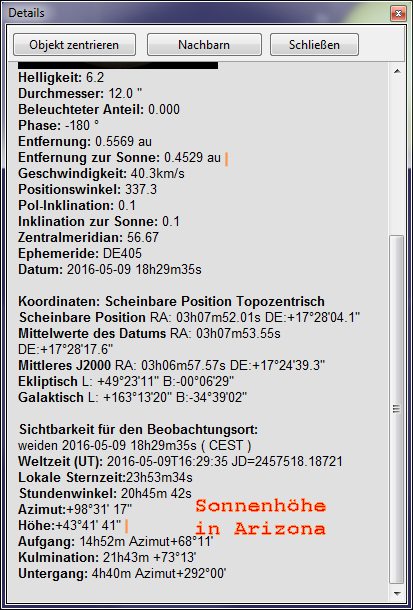
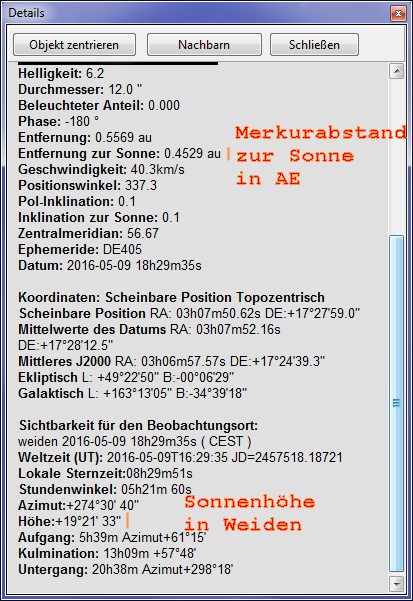
Dieser Wert entspräche dem Anblick aus der Richtung der Sonne wenn exakt zwischen den beiden Standorten Mittag wäre, denn dann wäre der Horizontabstand der Sonne an beiden Standorten gleich groß. Tatsächlich stand jedoch zum Aufnahmezeitpunkt in Weiden die Sonne nur 19,35 Grad über dem Horizont während es in BigBearCity 43,7 Grad gewesen sind. Die Differenz von 24,35 Grad verkürzt die Sichtlinie aus der Perspektive der Sonne auf cos(24,35)*8587,7. Das sind 7824 km.
Zur
Ermittlung der astronomischen Einheit wird zunächst der
Abstand
Merkur-Sonne in astronomischen Einheiten berechnet. Dies geschieht
über die Umlaufzeit mit dem dritten Keplerschen Gesetz. Die
Bahn
des Merkur ist jedoch stark elliptisch. Daher ist der reale Abstand
schwankend. Der Einfachheit halber wurde der Wert aus Cartes du Ciel
verwendet. Demnach lag der Sonnenabstand des Merkur am Transittag bei
0,4529 AE. Wer sich für die Berechnung nach Kepler
interessiert, kann sich die Messung zum Venustransit anschauen:
http://www.astrode.de/venustr2.htm
Die Errechnung der AE basiert auf dem Strahlensatz
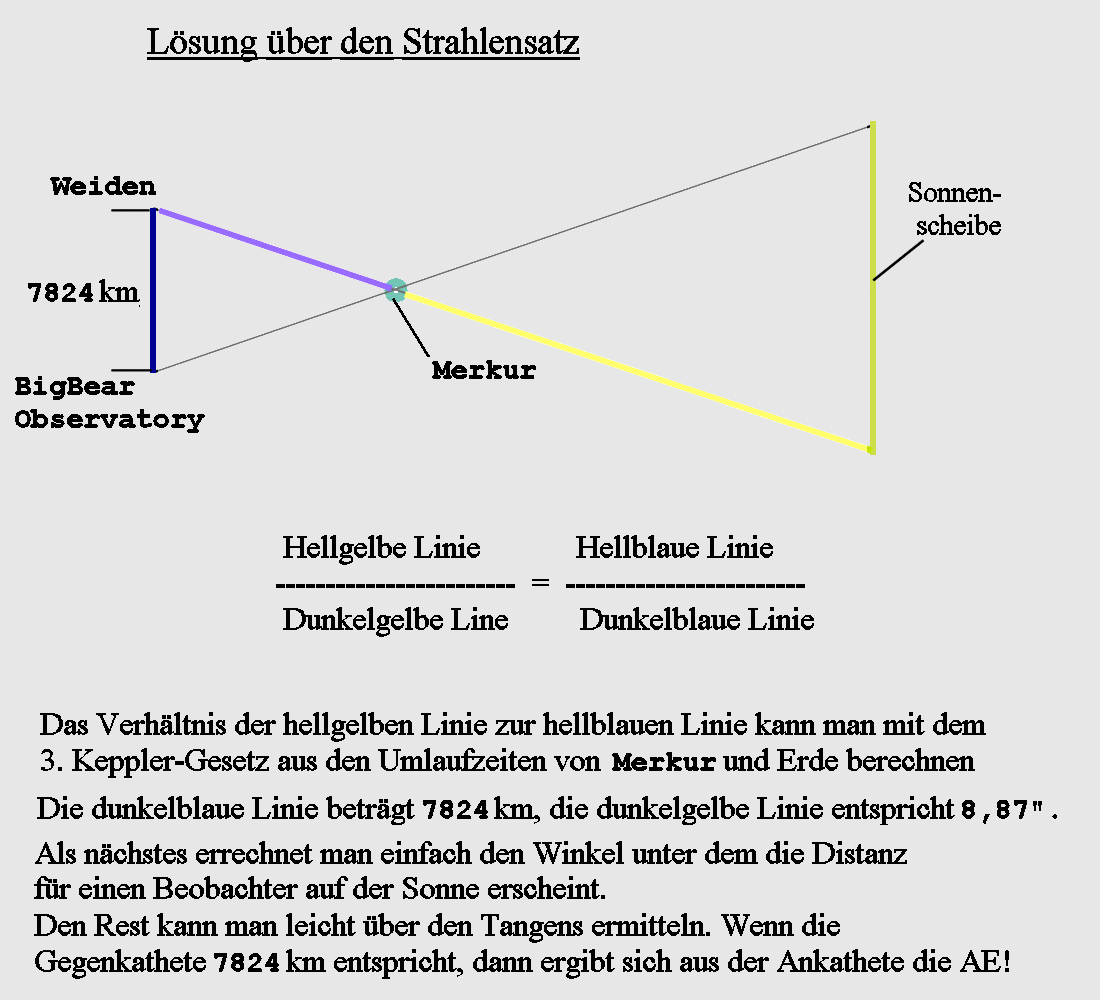
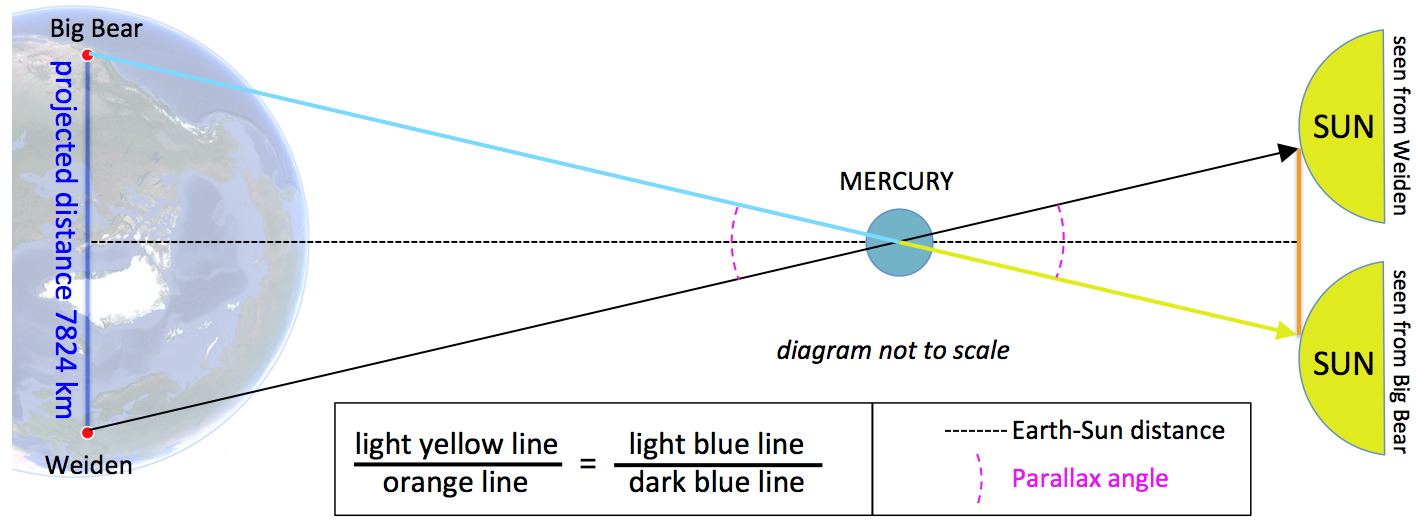
Nun wird
die Parallaxe der Sonne ermittelt. Sie entspricht dem halben Erdwinkel
aus der Sicht eines Beobachters auf der Sonne.
Sonnenparallaxe = ((1 / Abstand Merkur zur Sonne - 1) * Erddurchmesser
* 8,87 / 7824 / 2
Bei einem Erddurchmesser von 12757 km und einem Abstand Merkur-Sonne
von 0,4529 beträgt die Sonnenparallaxe 8,73 Bogensekunden. Die
AE
kann man nun mit dem Erddurchmesser direkt aus der Sonnenparallaxe
errechnen.
Astronomische Einheit = Erddurchmesser / tan (Sonnenparallaxe / 3600 *
2)
Heraus käme ein Wert von 150,7 Mio km.
Aufgrund der elliptischen Erdbahn war war der Erdabstand von der Sonne am Transittag größer als die astronomische Einheit von 149,6 Mio km. Sie lag bei 1,0097 AE oder 151,05 Mio km. Die Abweichung bei der Distanzbestimmung liegt bei nur 2,3 Promille!
Die hohe Genauigkeit ist wohl lediglich ein Zufallstreffer. Der Abstand der beiden Scheibchenmitten lässt sich bestenfalls auf 5% genau bestimmen. Daher muss von einem ähnlich hohen Fehlerbalken ausgegangen werden.

